DL-Q learning算法

路径规划
,

Q-learning简介

Q-learning算法是model- free的TD算法(Temporal Difference)之一。它的目的是让智能代理学习通过与环境互动来最大化累积奖励的最佳策略（optimal policy）。它的学习流程满足马尔可夫过程(MDP)。它属于值迭代（value iteration）方法，通过构建并更新“动作-状态价值函数”（Q函数），实现对环境的最优决策。

Q1. 什么是model-free？

  • **model-free（无模型）**意思是，该算法在学习如何做决策时 不需要提前知道环境的全部规则或转移概率。
  • 换句话说，Q-Learning 不需要知道“做了某动作后，环境会怎么变化”这个模型，它只是通过与环境的反复交互、实践操作，不断总结经验，来学会什么是好决策。
  • 相对的还有model-based（有模型）算法，这类算法需要先学习或者已经有一个环境的模型，即知道“在某一个状态采取某个动作后，下一步最可能到达哪个状态”，然后用这些信息做决策。

举例：

  • Model-free就像是在玩一个新游戏时，完全不知道规则，通过不断尝试和反馈，慢慢学会如何玩得更好。

  • Model-based就像是事先有攻略或说明书，已经知道每个决定背后的后果，然后用这些知识决策。

    这个地方的TD指的是边走边学，而不是等一整个回合结束。

Q-learning算法具体解读

  • Q-learning的核心思想

Q-learning的目标是学习一个最优的Q函数 ${Q^*(s, a)}$，定义在状态 ${ s }$ 和动作 ${ a }$ 上，反映在状态 ${ s }$ 下采取动作 ${ a }$ 后能获得的最大期望回报（reward）。

最优Q函数满足贝尔曼最优方程。 方程为：

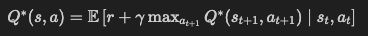
Bellman equation

其中：

  • ${ r }$：执行动作 ${ a }$ 后获得的即时奖励
  • ${ \gamma }$：折扣因子（ ${ 0 < \gamma < 1 }$ ）
  • ${ s_{t+1} }$：执行动作后的下一个状态
  • ${ a_{t+1} }$：下一个状态可能采取的动作

3. 算法流程

核心步骤如下：

  1. 随机初始化 Q 表（ ${ Q(s, a) }$ ）
  2. 重复以下过程（直至收敛）：
    • 在当前状态 ${ s_t }$ 选择动作 ${ a_t }$（通常采用 ${\epsilon}$-贪婪策略）
    • 执行动作 ${ a_t }$，获得奖励 ${ r_{t+1} }$ 并转移到下一个状态 ${ s_{t+1} }$
    • 更新 Q 表：Q表格的更新使用下面的公式

${
Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right]
}$

其中：

  • ${ \alpha }$：学习率（ ${ 0 < \alpha \leq 1 }$ ）
  • ${ \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) }$：对下一个状态选择价值最大的动作
  • ${ r_{t+1} + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) }$：目标值
  • ${ Q(s_t, a_t) }$：当前估计
  1. 将状态更新为 ${ s_{t+1} }$，继续上述过程

其中 ${
\left [ r_{t+1} + \gamma \max_{a_{t+1}} Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right]
}$ 这个整体叫做 TD error，用来衡量 Q 表的更新是否偏离了真实的 Q 值。

4. 算法特性

  • Q-learning是离线、无模型、值函数型强化学习方法。
  • 能够在未知环境中通过试错学习最优策略。
  • 最终收敛于最优Q函数，只要每个动作在每个状态都有无限次被探索的机会。

Q-learning伪代码

数学公式-Q值更新公式（时序版本）：

${
Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a) - Q(s_t, a_t) \right]
}$

输入：

  • S：状态空间
  • A：动作空间
  • α（alpha）：学习率 (0 < α ≤ 1)
  • γ（gamma）：折扣因子 (0 < γ < 1)
  • ε（epsilon）：探索率 (0 ≤ ε ≤ 1)
  • max_episodes：最大回合数
  • max_steps：每回合最大步数

初始化：
对每一对 (s, a) ∈ S × A，初始化 Q(s, a) ← 任意值（如0），但是大部分论文都利用欧氏距离的倒数来初始化这个Q表格。这样可以加速收敛。

算法主体：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
输入：学习率 α，折扣因子 γ，探索率 ε，最大回合数 max_episodes，最大步数 max_steps
初始化 Q(s, a)，对所有状态-动作对赋初值

for episode = 1 to max_episodes do
    初始化起始状态 s₀

    for t = 0 to max_steps-1 do
        按 ε-贪婪策略选择动作 aₜ：
            - 以概率 ε：随机选择 aₜ
            - 以概率 1-ε：选择最大 Q 值对应的 aₜ
        执行动作 aₜ，获得奖励 rₜ₊₁ 和新状态 sₜ₊₁，done 指示是否终止

        Q(sₜ, aₜ) ← Q(sₜ, aₜ) + α [rₜ₊₁ + γ * maxₐ Q(sₜ₊₁, a) - Q(sₜ, aₜ)]

        若 done == True:
            跳出当前回合

        状态转移: sₜ ← sₜ₊₁

    （可选）ε随回合数进行衰减

输出：Q(s, a)

最终策略 π(s):
    π(s) = argmaxₐ Q(s, a)