快速探索随机树RRT

路径规划
,

RRT（Rapidly-exploring Random Tree）

一、简介

快速探索随机树（RRT, Rapidly-exploring Random Tree）是一种高效的采样型路径规划算法，于1998年由Steven M. LaValle提出。RRT擅长于高维空间中寻找从起点到终点的可达路径，被广泛应用于机器人路径规划、智能车辆导航、机械臂运动学等领域。

二、核心思想

RRT利用随机采样点，在空间中快速扩展一棵树，逐步探索工作空间。每次采样后，树都是从“离采样点最近的已有节点”朝向新采样点延伸，最终使得整棵树能覆盖到目标区域。

特性：

  • 快速、高效地探索空间。
  • 不要求环境空间网格化，适合高自由度问题。

三、基本流程

  1. 初始化树
    以起点s_start为根节点，建立一棵空树$T$。

  2. 循环扩展（直到步数或找到目标为止）

    1. 在空间中随机采样点（大部分为随机点，少部分直接采样终点，后者称为goal biasing）。
    2. 找到树中与采样点最近的节点$nearest$。
    3. 从$nearest$朝采样点方向生长最大步长$\delta_{\mathrm{max}}$，生成新节点$new$。
    4. 如果$nearest$到$new$之间路径无障碍，将$new$插入树，并设置父节点为$nearest$。
    5. 判断$new$是否已接近终点，若从$new$到终点无障碍，加入终点节点，结束循环。

  3. 路径回溯
    从终点开始，根据父节点信息逐步回溯到起点，得到整条可行路径。

四、例子

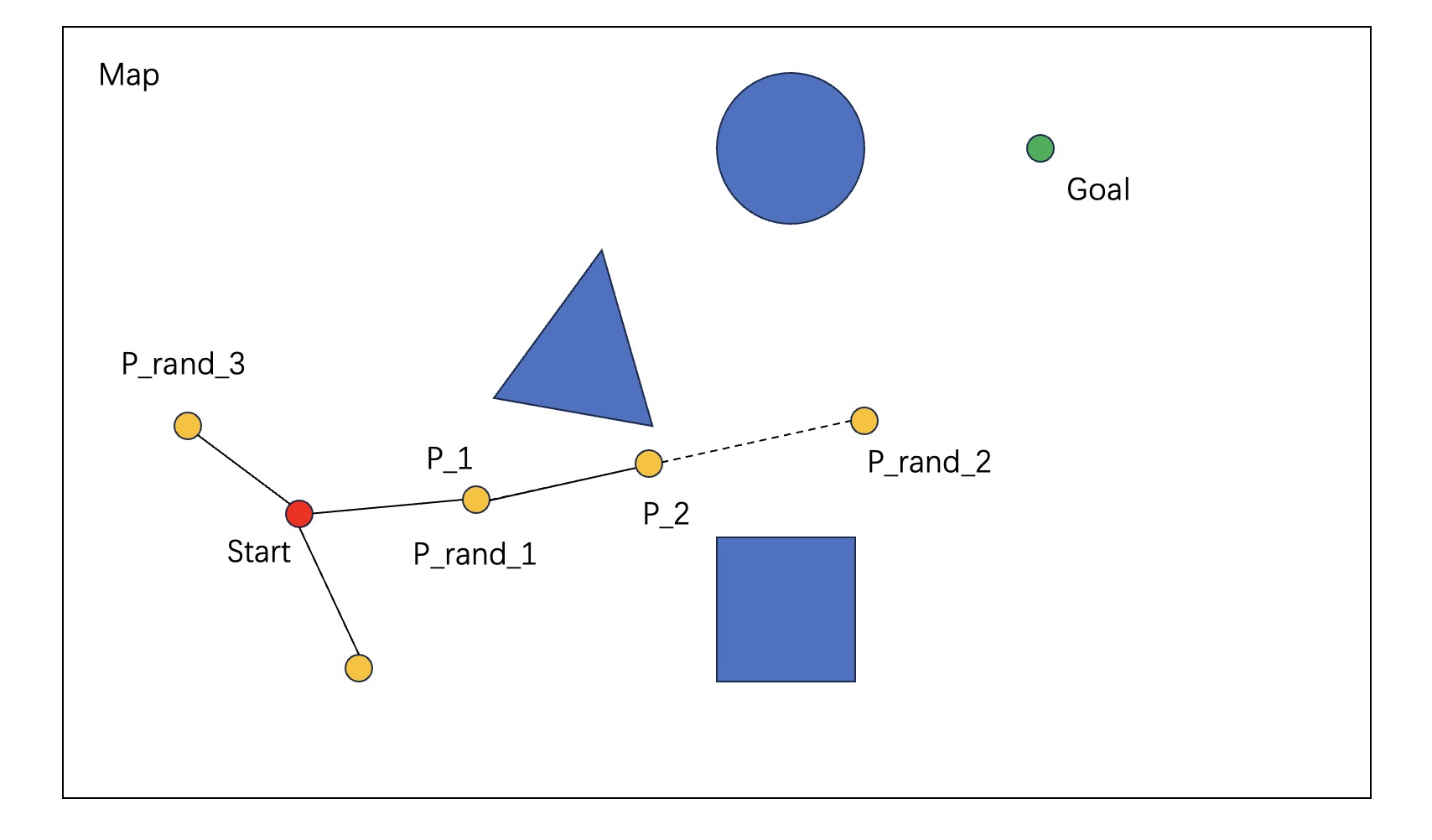
RRT example

如上图所示，首先从起点开始，每次随机生成一个点。如果生成的点 P_rand 和树上最近的节点 P_nearest 之间的连线 Line(P_rand, P_nearest)不会和障碍物碰撞。如果距离d(P_rand, P_nearest)小于设置的最大步长$\delta_{\mathrm{max}}$，那么将这个点加入到树中（比如: P_rand_1, P_rand_3）。 如果不碰撞但是距离d(P_rand, P_nearest)大于步长$\delta_{\mathrm{max}}$，那么就朝着P_rand的方向走最大步长（比如：P_rand_2和P_1之间距离太大，那么朝着P_rand_2方向走到了P_2的位置）；相反，如果一开始就会碰撞，那么直接淘汰。

关于随机采样点可能存在的疑惑：大部分为随机点，少部分直接采样终点，后者称为goal biasing.

  • 因为我们需要在这个扩展的过程中直接采样终点从而引导这个路径向着终点的方向前进。如果只是随机，很可能采样非常多次才可能达到终点。

五、RRT算法伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def RRT(start, goal, max_iter, delta, goal_sample_rate):
    tree = {start: None}    # 节点:父节点
    for i in range(max_iter):
        # 随机采样 goal_sample_rate ---> 采用终点的频率
        if random.random() > goal_sample_rate:
            sample = random_sample_point()
        else:
            sample = goal
        
        nearest = find_nearest(tree, sample)
        new = steer(nearest, sample, delta)
        
        if not collision(nearest, new):
            tree[new] = nearest

            # 检查是否到达目标
            if distance(new, goal) < delta and not collision(new, goal):
                tree[goal] = new
                break
    # 路径回溯
    path = [goal]
    while path[-1] != start:
        path.append(tree[path[-1]])
    path.reverse()
    return path

五、关键参数说明

  • 采样点概率goal_sample_rate：通常设置为0.05，保证有一定概率直接引导树朝目标生长，加速收敛。
  • 步长delta：控制树每次扩展的距离，太大会跳过障碍，太小会导致效率降低。
  • 最大迭代步数max_iter：限制RRT运行时间，也影响能否找到路径。

六、优缺点

  • 优点

    • 非常适合高维空间问题，不需要先验网格。
    • 能处理非线性、多障碍环境。
    • 简单、高效，易于实现和移植。
    • 可以不断增加采样次数，无需预设所有节点。

  • 缺点

    • 路径通常不是最优解（仅是可行解）。
    • 在窄通道等复杂环境下效率变差，很多时候得到的结果是贴着障碍物的边缘。
    • 路径往往有锯齿，不满足动力学可行性、不光滑，需要后处理（如B样条、Path Smoothing等）。

参考文献

  • Steven M. LaValle. Rapidly-Exploring Random Trees: A New Tool for Path Planning, 1998.